Kamis, 12 November 2015

Rumus Trigonometri

Posted By: ArumFetria - 21.10
Soal Latihan :

1. tan (x+y) / cos x cos y = tan x + tan y
2. sin (x-y) / tan x - tan y = cos x cos y
3. sin (x+y) . sin (x-y) = sin^2 x - sin^2 y
4. sin(x+y) - sin(x-y) / cos (x+y) + cos (x-y) = tan y
5. BC=CD=1 satuan. Gunakan rumus sin (A+B) untuk menunjukkan bahwa V3 sin a + cos a = 4 / V7


Soal Latihan 2 :
1. Di ketahui sin x = 1/2, dan x sudut di kuadran pertama, hitunglah :
a. Cos x
b. Tan x
(ket : x = alpa)
~
2. Diketahui cos A = - 4/5 dan A sudut dikuadran ketiga. Hitung :
a. Sin A (aku dapat hasilnya = - akar 9/25)
b. Tan A (aku dapat hasilnya = akar 9/16)
~
3. Jika sin x = 12/13 dan cos y = 24/25 (x dan y masing masing sudut lancip). Hitunglah :
a. Cos x
b. Tan x
c. Sin y
d. Tan y
e. Sin x Cos y - Cos x Sin y
f. Cos x Cos y - Sin x Sin y
g. Tan x + Tan y = 1 - Tan x Tan y

Pembahasan :
1.] sin x = 1/2 , x = 30°
a.) cos x = cos 30 = (1/2)√3
b.) tan x = tan 30 = (1/3)√3

2.] cos A = -4/5 , A = 217°
a.) sin A = sin 217 = -3/5
b.) tan A = tan 217 = 3/4

3.] sin x = 12/13 , cos y = 24/25, gunakan aturan segitiga siku-siku
a.) cos x = 5/13
b.) tan x = 12/5
c.) sin y = 7/25
d.) tan y = 7/24
e.) = sin x cos y - cos x sin y
= (12 . 24) / (13 . 25) - (5 . 7) (13 . 25)
selesaikan sendiri yaa
f.) = cos x cos y - sin x sin y
= (5 . 24) / (13 . 25) - (12 . 7) / (13 . 25)
selesaikan sendiri yaa
e.) tan x + tan y = 1 - tan x tan y
= tan (x + y)


Soal Latihan 3 :

Jika tan x + tan y = 25 dan cot x + cot y = 30, maka nilai tan (x + y) adalah

Rumus trigonometri umum
Sudut-Sudut Istimewa sin cos tan 0 30 45 60 90 derajat
Aturan sin cos tan lain


Rumus-rumus Trigonometri pada segitiga dengan sisi a b c
Aturan sinus

Aturan Cosinus

Luas Segitiga 2 sisi dan 1 sudut

Luas segitiga dengan 3 sisi akan dibahas lain waktu
Rumus jumlah 2 sudut trigonometri sin cos tan

sepertinya gambar ini ada yang salah, nanti diperbaiki
Sudut 2A atau sin 2x, cos 2x, tan 2x
Rumus kali trigonometri sin cos cos sin cos cos -sin sin
Rumus jumlah 2 trigonometri sin cos cos sin cos cos -sin sin
Persamaan Trigonometri mudah sekali dikerjakan
Bentuk a Cos x + b Sin x = k cos x-teta
Bentuk a Cos x + b Sin x = c
Nilai Maksimum dan Minimum Fungsi f(x) =a Cos x + b Sin x


yang ini sering juga keluar di soal snmptn



Fungsi dasar:
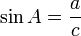
\sin A = \frac{a}{c}\,
\cos A = \frac{b}{c}\,
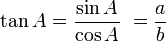
\tan A = \frac{\sin A}{\cos A}\ = \frac{a}{b}\,
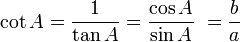
\cot A = \frac{1}{\tan A} = \frac{\cos A}{\sin A}\ = \frac{b}{a}\,
\sec A = \frac{1}{\cos A}\ = \frac{c}{b}\,
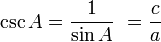
\csc A = \frac{1}{\sin A}\ = \frac{c}{a}\,


Rumus setengah sudut

\sin \frac{A}{2} = \pm \sqrt{\frac{1-\cos A}{2}} \,
\cos \frac{A}{2} = \pm \sqrt{\frac{1+\cos A}{2}} \,
\tan \frac{A}{2} = \pm \sqrt{\frac{1-\cos A}{1+\cos A}} = \frac {\sin A}{1+\cos A} = \frac {1-\cos A}{\sin A} \,

Rumus sudut rangkap tiga

\sin 3A = 3 \sin A - 4 \sin^3 A \,
\cos 3A = 4 \cos^3 A - 3 \cos A \,

Rumus sudut rangkap dua

\sin 2A = 2 \sin A \cos A \,
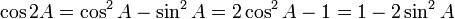
\cos 2A = \cos^2 A - \sin^2 A = 2 \cos^2 A -1 = 1-2 \sin^2 A \,
\tan 2A = {2 \tan A \over 1 - \tan^2 A} = {2 \cot A \over \cot^2 A - 1} = {2 \over \cot A - \tan A} \,

Penjumlahan

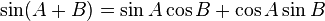
\sin (A + B) = \sin A \cos B + \cos A \sin B \,
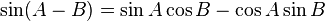
\sin (A - B) = \sin A \cos B - \cos A \sin B \,
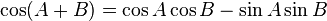
\cos (A + B) = \cos A \cos B - \sin A \sin B \,
\cos (A - B) = \cos A \cos B + \sin A \sin B \,
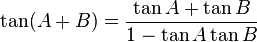
\tan (A + B) = \frac{\tan A + \tan B}{1 - \tan A \tan B} \,
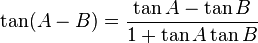
\tan (A - B) = \frac{\tan A - \tan B}{1 + \tan A \tan B} \,
2 \sin A \times \cos B = \sin (A + B) + \sin (A - B),
2 \cos A \times \sin B = \sin (A + B) - \sin (A - B),
2 \cos A \times \cos B = \cos (A + B) + \cos (A - B),
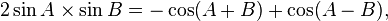
2 \sin A \times \sin B = - \cos (A + B) + \cos (A - B),

Identitas trigonometri

\sin^2 A + \cos^2 A = 1 \,
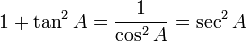
1 + \tan^2 A = \frac{1}{\cos^2 A} = \sec^2 A\,
1 + \cot^2 A = \frac{1}{\sin^2 A} = \csc^2 A \,


SUMBER                  
http://ilmu-duniadanakhirat.blogspot.co.id/2012/11/kumpulan-rumus-trigonometri-dan-harga-sin-cos-tan.html
Filled Under

About ArumFetria

Organic Theme is officially developed by Templatezy Team. We published High quality Blogger Templates with Awesome Design for blogspot lovers.The very first Blogger Templates Company where you will find Responsive Design Templates.

0 komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)

Copyright © arumfe

Designed by